Algorithms for animating AllRGB images
AllRGB is a really cool challenge: make an image that contains each of the 16777216 RGB colors exactly once.
I wrote a HTML canvas-based visualization of an AllRGB image being created. It uses several space-filling curves in 2D and 3D.
I made a demo of this at /projects/allrgb and the source is on GitHub.
Mapping cubes and planes to a line
My goal: traverse the RGB cube and also traverse the square pixel plane in an interesting way. In other words, create a list of 2563 unique 3D coordinates (representing 24-bit RGB colors) and a list of 40962 unique 2D coordinates (representing pixel locations).
I chose these traversal algorithms:
- Cube traversal
- Depth-first search (3D DFS)
- Serpentine (3D)
- Plane traversal
- Moore curve (a variant of the Hilbert curve)
- Depth-first search (2D DFS)
- Serpentine (2D)
Example: Serpentine
Serpentine traversal is the simplest traversal algorithm I had. Note that it is not a space filling 'curve': it jumps after finishing a row, so it's not continuous.
Pseudocode for plane traversal
y = 0
while y < 4096:
x = 0
while x < 4096:
print (x, y)
x = x + 1
y = y + 1
RGB cube traversal is a bit more interesting. While this can be implemented this as three nested loops, an easier solution is to convert the input number to hexadecimal.
// converts an integer n from [0..16777215] into the corresponding hex color (#RRGGBB)
function getColor(n) {
return '#' + n.toString(16).padStart(6, '0');
}
Example: Moore curve

By Robert Dickau [CC BY-SA 3.0], via Wikimedia Commons
This was the most interesting traversal algorithm I did. The Moore curve is a space-filling fractal, the loop variant of the Hilbert curve.
It can be represented as a Lindenmayer rewrite system:
- Variables:
L,R - Constants:
F,+,− - Axiom:
LFL+F+LFL - Production rules:
L→−RF+LFL+FR−R→+LF−RFR−FL+
If you apply these rules recursively to the axiom, you get a set of instructions for moving a turtle. The instructions are string of constants where each character has the following meaning:
F: draw at current location and move forward in current direction+: turn right 90°-: turn left 90°
This is a recursive function to generate L-system instructions:
function generateInstructions(level) {
if (level === 0) { // base case
// return axiom to start the instructions
return 'LFL+F+LFL';
}
// recursive case
let instructions = generateInstructions(level - 1);
// replace 'L's and 'R's with their respective production rules
// 'X' is a temporary variable representing the original Ls
return instructions.replace(/L/g, 'X')
.replace(/R/g, '+LF-RFR-FL+')
.replace(/X/g, '-RF+LFL+FR-');
}
After cleaning up the final instructions, you get this:
> // clean up the instructions by replacing useless parts like +-, -+, R, and L
> generateInstructions(3).replace(/(\-\+)|(\+\-)|R|L/g, '')
"-F+F+F-FF-F-F+F+F-F-FF-F+F+FF+F-F-F+FF+F+F-F-F+F+FF+F-F-FFF-F-F+FF+F+F-F-F+F+FF+
F-F-F+FF+F+F-FF-F-F+F+F-F-FF-F+F+F-F-F+F+F-FF-F-F+F+F-F-FF-F+F+FF+F-F-F+FF+F+F-F-
F+F+FF+F-F-FFF-F-F+FF+F+F-F-F+F+FF+F-F-F+FF+F+F-FF-F-F+F+F-F-FF-F+F+FFF+F+F-FF-F
-F+F+F-F-FF-F+F+FF+F-F-F+FF+F+F-F-F+F+FF+F-F-FFF-F-F+FF+F+F-F-F+F+FF+F-F-F+FF+F+
F-FF-F-F+F+F-F-FF-F+F+F-F-F+F+F-FF-F-F+F+F-F-FF-F+F+FF+F-F-F+FF+F+F-F-F+F+FF+F-F
-FFF-F-F+FF+F+F-F-F+F+FF+F-F-F+FF+F+F-FF-F-F+F+F-F-FF-F+F+F-"
To traverse the full pixel plane, I needed an instruction set with exactly 40962 = 16777216 'draw' instructions. (There is an implicit F at the beginning of the instruction set, so I actually needed 16777215 Fs.) The following table shows that I needed to recurse 11 times for this.
| Recursion Level | instructions.length | Num of Fs |
|---|---|---|
| 0 | 9 | 3 |
| 1 | 49 | 15 |
| 2 | 209 | 63 |
| 3 | 849 | 255 |
| 4 | 3409 | 1023 |
| 5 | 13649 | 4095 |
| 6 | 54609 | 16383 |
| 7 | 218449 | 65535 |
| 8 | 873809 | 262143 |
| 9 | 3495249 | 1048575 |
| 10 | 13981009 | 4194303 |
| 11 | 55924049 | 16777215 |
Strategy design pattern
This was intended to be a quick project, so I would have normally made each of the traversers into a function in script.js, but I wanted to organize my code better. It made the most sense to separate out the code for the traversers, so I decided to use the strategy design pattern.
Each of the traversers (both cube and plane) has a very similar interface. They need a function to return their name and another to return the next traversed value.
Strategy design pattern code:
// Interface for Traverser strategy
class Traverser {
constructor(LEVEL, CANVAS_GRID_SIZE) {/* */}
getName() {/* */}
*generator() {/* */}
}
// Maps names to strategies
const traversers = {
plane: {
'serpentine': SerpentinePlane,
'moore': MoorePlane,
'dfs': DepthFirstSearchPlane,
},
cube: {
'serpentine': SerpentineCube,
'dfs': DepthFirstSearchCube,
'hsl': HslCube,
}
};
// ...
// Creates new objects, representing traversal strategies
const planeTraverser = new traversers.plane['moore'](level, gridSize);
const cubeTraverser = new traversers.cube['dfs'](level, gridSize);
JavaScript generators

I initially implemented all my traversers as plain functions, but that had a lot of messy recalculation and non-local variables. Then I learned about a fancy newish feature in JavaScript called generators. Generators are well supported in modern browsers, so I felt safe using them in my project.
Using generators made my code more memory-efficient and cleaner.
Example of plane traverser using a generator:
// Generator that returns an RGB color
function* serpentine() {
for (let n = 0; n < 16777216; n++) {
yield "#" + n.toString(16).padStart(6, "0");
}
}
// ...
let planeTraverser = serpentine();
planeTraverser.next(); // {value: "#000000", done: false}
planeTraverser.next(); // {value: "#000001", done: false}
Results!
Moore plane + DFS cube is my favorite.
| DFS plane | Moore plane | Serpentine plane | |
|---|---|---|---|
| DFS cube |  |  |  |
| Serpentine cube |  |  | 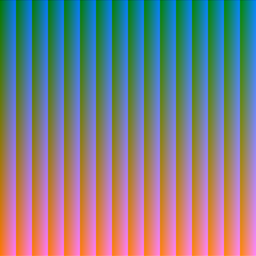 |
- Demo: /projects/allrgb
- Source: GitHub
